Fonction de survie

28 Novembre 2021

Les fonctions de survie sous R

Introduction
Quelques distributions
Estimation de Kaplan-Meier
Modèles à temps discret
Modèle de régression paramétrique
Proportional Hazard (PH) models
Accelerated Failure Time (AFT) models
Autres modèles
Cox Proportional Hazard

Introduction

Définitions et exemples :

On s'intéresse ici à des variables de survie : une variable de survie, c'est à peu près comme une variable quantitative, mais elle peut prendre des valeurs numériques précises, comme "13 ans", mais aussi des valeurs moins précises, du genre "plus de 15 ans".

On qualifie de "valeurs censurées" ces valeurs moins précises. On les note généralement ainsi :

10+    Plus de 10 (donnée censurée à droite)
5-     Moins de 5 (censurée à gauche)
[5,10] Entre 5 et 10

On les rencontre par exemple quand on regarde la durée de survie après un cancer : si l'étude dure 10 ans, on pourra donner la durée de survie de tous les patients qui sont morts, mais pour les autres, on pourra juste dire que leur durée de survie est supérieure à 10 ans. La censure à gauche correspond à des évènements qui ont eu lieu avant le début de l'étude (mais tous les individus ne rentrent pas dans l'étude en même temps). A FAIRE : donner un exemple concret de censure à gauche. La censure par intervalle se rencontre par exemple quand on constate l'apparition d'un symptome lors d'une visite médicale : il est apparu depuis la visite précédente, mais on ne sait pas exactement quand.

Voici d'autres exemples : durée de survie d'un patient, durée de survie d'un mariage, durée de survie d'une entreprise, durée de fonctionnement sans panne d'un produit manufacturé, durée pendant laquelle un produit reste suffisemment populaire pour continuer à être produit, durée de survie d'un enseignant en lycée (jusqu'à sa démission, son internement en hopital psychiatrique, son suicide), durée jusqu'à l'arret de prise d'un médicament, etc.

On peut aussi voir les variables de survie comme des variables qualitatives binaires (celles qu'on cherche à prédire dans la régression logistique) indiquant la survenue ou non d'un évènement, auxquelles on a ajouté l'instant de survenue de cet évènement. Les valeurs censurées correspondent à << l'évènement ne s'est pas produit >> : dans les exemples précédents, cela revient à remplacer les valeurs << Vivant / Mort >> par << Vivant / Date de la mort >>.

Les variables de survie peuvent avoir plusieurs valeurs : par exemple sain, malade et mort (si un patient guérit entre deux maladies, ça devient encore plus compliqué). Dans ces situations plus complexes, on parle parfois de données transitionnelles (car on s'intéresse à la transition d'un état vers un autre) ou de "spell duration data".

On peut aussi voir une donnée de survie comme une série temporelle qualitative, dans laquelle on s'intéresse aux transitions d'un état à l'autre.

A FAIRE :

Competing risk models
Un état de départ et plusieurs états absorbants
(exemple : passage du chomage à un emploi ou du chomage à une sortie
du marché de l'emploi ; autre exemple : concurrence entre mort du
cancer et mort de maladie cardiovasculaire).

Survival function, Hazard function

Si T est une variable de survie, sa fonction de survie est

S(t) = P(T>t) = 1-F(t).

Par exemple, si T désigne le nombre d'années de survie après la diagnostic d'un cancer, S(t) est la probabilité de survivre au moins t années.

Sa "hazard function", ou "hazard rate" (je ne sais pas comment on dit en français : fonction de risque ?) est

                    P( t < T <= t + u | T > t )
lambda(t) =  lim   -----------------------------
            u -> 0              u

             dF/dt
          = -------
               S

               d ln S
          = - --------
                 dt

La formule ressemble beaucoup à la définition de la densité, mais on a ajouté la condition "T>t".

A la différenciation près, c'est très semblable à la différence entre l'espérance de vie à la naissance et l'espérance de vie à 60 ans, ou la différence entre la probabilité de mourir entre 12 et 13 ans et la probabilité de mourir entre 12 et 13 ans sachant que le patient a déjà survécu 12 ans.

On rencontre aussi parfois la "cumulative hazard function", primitive de la précédente, qui représente le risque cumulé.

Lambda(t) = - ln S(t)

Quelques distributions

Distribution exponentielle

Elle correspond à une "hazard function" constante,

lambda(t) = lambda
Lambda(t) = lambda t
S(t) = exp( - lambda t )

op <- par(mfrow=c(3,1))
n <- 20
lambda <- rep(2,n)
x <- seq(0,2,length=n)
plot(lambda ~ x, type='l', main=expression(lambda))
plot(lambda*x ~ x, type='l', main=expression(Lambda))
plot(exp(-lambda*x) ~ x, type='l', main="S")
par(op)

Distribution de Weibull

Elle correspond à une "hazard function" de la forme

Lambda(t) = a * t ^ gamma
S(t) = exp( - a * t ^ gamma )

op <- par(mfrow=c(3,1))
n <- 20
alpha <- 1
g <- rep(2,n)
x <- seq(0,2,length=n)
plot(g * alpha * x^(g-1) ~ x, type='l', main=expression(lambda (gamma==2)))
plot(alpha * x^g ~ x, type='l', main=expression(Lambda))
plot(exp(-alpha*x^g) ~ x, type='l', main="S")
par(op)

Distribution log-normale

A FAIRE : expliquer

op <- par(mfrow=c(3,1))
n <- 200
x <- seq(0,5,length=n)
plot(1-plnorm(x) ~ x, type='l', main="S")
L <- function (x) { -log(1-plnorm(x)) }
plot(L(x) ~ x, type='l', main=expression(Lambda))
h <- .001
plot( (L(x+h)-L(x))/h ~ x, type='l', main=expression(lambda))
par(op)

Autres modèles

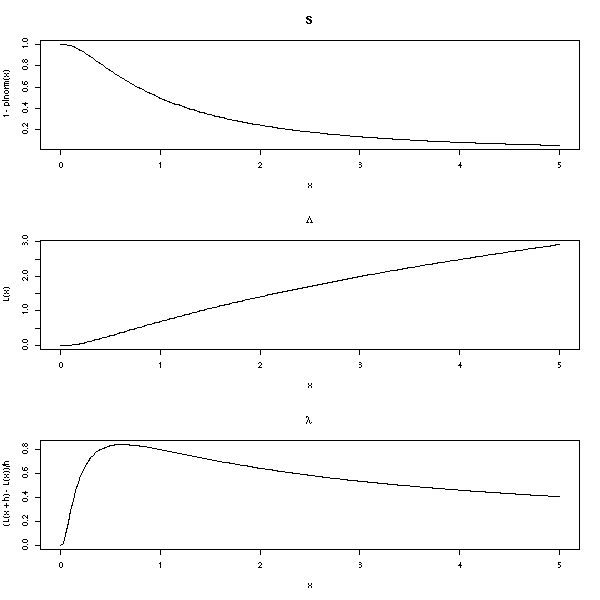
Weibul: lambda = alpha * t^(alpha-1) * exp(+X béta)
???
A FAIRE : il y a une variable prédictive, qui n'a pas encore sa
place ici...

log-logistic model:

                  1
S(t) = --------------------------  with lambda = exp(- X béta)
        1 + (lambda t)^(1/gamma)


Gompertz: lambda = exp( exp(+X béta) + gamma t )
(important)

Generalized Gamma
(généralise les modèles précédents: kappa=1:Weibul,
kappa=0:lognormal, kappa=sigma:gamma)

Il y a aussi des modèles à temps discret :

logistic
complementary log-log

Estimation de Kaplan-Meier

Estimation de la fonction de survie selon Kaplan--Meier (product-limit Kaplan--Meier estimator)

S'il n'y a pas de censure, on peut estimer la fonction de survie ainsi :

        Card( i : T_i>t )
S(t) = -------------------
              n

En présence de censure, on tient compte des données censurées jusqu'à ce qu'on arrive à leur valeur, et après on les oublie. Plus précisément, si le temps est discret :

S(t0) = P(vivant à t=t0 | vivant à t=t0-1) * P(vivant à t=t0-1)

Par exemple, la fonction de survie de la série

1 2 2 2+ 3+ 3+ 3+ 4 4 4 4 ... (100 individus)

se calcule ainsi :

temps sujets morts censures       p1     p2    S=p1*p2
------------------------------------------------------
1        100     1        0   99/100      1        .99 
2         99     2        1   97/100    .99      .9603
3         96     0        3   96/100  .9603      .9219
4         93     3        0   90/100  .9219      .8297

Les valeurs de S sont des produits de plus en plus gros :

S(0) = 1
S(1) = 1 * 99/100
S(2) = 1 * 99/100 * 97/100
S(3) = 1 * 99/100 * 97/100 * 96/100
S(4) = 1 * 99/100 * 97/100 * 96/100 * 90/100
etc.

On peut donner une formule générale :

                              di
S(t) =    Produit      ( 1 - ---- )
       i tel que ti<t         ni

On peut calculer des intervalles de confiance en supposant que Lambda (qui vaut -log(S)) est normale.

A FAIRE : comment a-t-on la variance de Lambda ???

Il existe d'autres estimateurs de la fonction de survie, par exemple celui d'Altschuler--Nelson--Aalen--Flemming--Harrington :

                             di
Lambda(t) =      Somme     ------.
            i tel que ti<t   ni

Ces estimateurs ont une variance élevée : si on a un modèle raisonnable, il vaut mieux préférer un estimateur paramétrique obtenu par le maximum de vraissemblance (on peut signaler que l'estimateur de Kaplan--Meier correspond à un maximum de vraissemblance (non paramétrique)).

Analyse de survie sous R

La plupart des fonctions sont dans le paquetage "survival".

La commande Surv permet de créer des variables de survie.

> Surv(c(1,2,2,2,3,3,3,4,4,4,4),
+      c(1,1,1,0,0,0,0,1,1,1,1))
[1] 1  2  2  2+ 3+ 3+ 3+ 4  4  4  4

La commande survfit permet de calculer la fonction de survie.

> x <- Surv(c(1,2,2,2,3,3,3,4,4,4,4),
+           c(1,1,1,0,0,0,0,1,1,1,1))

> survfit(x)
Call: survfit(formula = x)
        n    events     rmean se(rmean)    median   0.95LCL   0.95UCL
   11.000     7.000     3.364     0.322     4.000       Inf       Inf

> summary(survfit(x))
Call: survfit(formula = x)
 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    1     11       1    0.909  0.0867        0.754            1
    2     10       2    0.727  0.1343        0.506            1
    4      4       4    0.000      NA           NA           NA

ou de la tracer

set.seed(87638)
library(survival)
n <- 200
x <- rweibull(n,.5)
y <- rexp(n,1/mean(x))
s <- Surv(ifelse(x<y,x,y), x<=y)
plot(s) # peu informatif

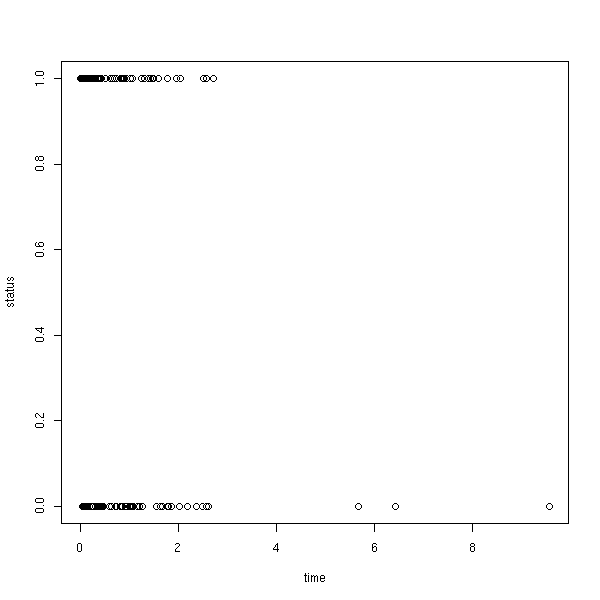
plot(survfit(s))
lines(survfit(s, type='fleming-harrington'), col='red')
r <- survfit(s)
lines( 1-pweibull( r$time, .5 ) ~ r$time, lty=3, lwd=3, col='blue' )
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
        c("Kaplan-Meier", "Fleming-Harrington", "Fonction de survie théorique"),
        lwd=c(1,1,3), lty=c(1,1,3),
        col=c(par("fg"), 'red', 'blue'))
title(main="Fonction de survie (estimation de Kaplan-Meier)")

op <- par(mfrow=c(3,1))
r <- survfit(s)
plot(r$surv ~ r$time, type='l', main="S")
curve( 1-pweibull(x,.5,1), col='red', lty=2, add=T )
plot(-log(r$surv) ~ r$time, type='l', main=expression(Lambda))
curve( -log(1-pweibull(x,.5,1)), col='red', lty=2, add=T )
# Avant de dériver, on commence par lisser Lambda
a <- -log(r$surv)
b <- r$time
library(modreg)
l <- loess(a~b)
bb <- seq(min(b),max(b),length=200)
aa <- predict(l, data.frame(b=bb))
plot( diff(aa) ~ bb[-1], type='l', main=expression(lambda) )
aa <- -log(1-pweibull(bb,.5,1))
lines( diff(aa) ~ bb[-1], col='red', lty=2 )
par(op)

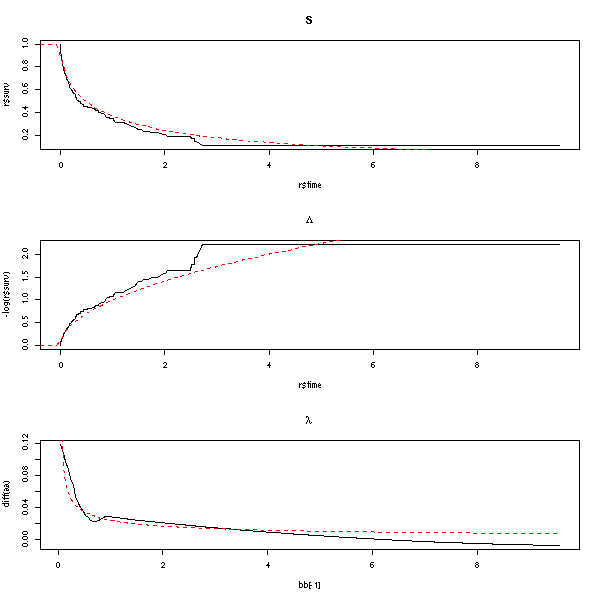
Remarque : on peut obtenir certains des graphiques ci-dessus en modifiant l'option "fun".

plot(r, fun="log", main="log-survival curve")

plot(r, fun="event", main="cumulative events: f(y)=1-y")

plot(r, fun="cumhaz", main="cumulative hazard: f(y)=-log(y)=Lambda")

try(
  plot(r, fun="cloglog", main="complementary log-log plot")
)
# f(y)=log(-log(y)), log-scale on the x-axis

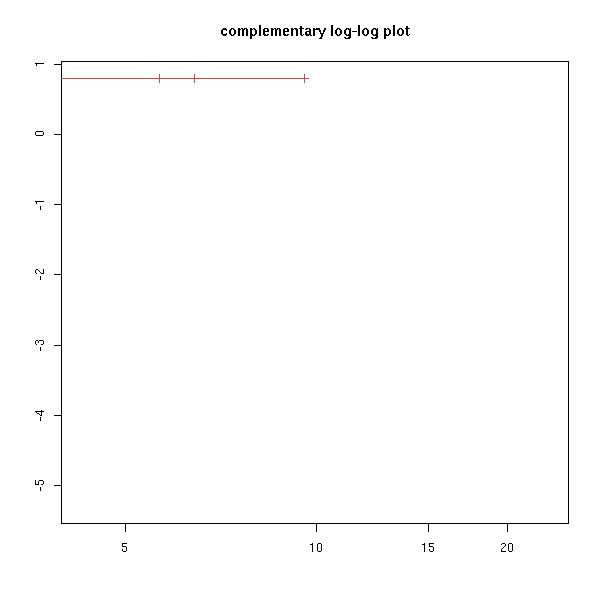
On peut aussi avoir un (ou plusieurs) facteurs -- nous en reparlerons plus loin.

n <- 200
x1 <- rweibull(n,.5)
x2 <- rweibull(n,1.2)
f <- factor( sample(1:2, n, replace=T), levels=1:2 )
x <- ifelse(f==1,x1,x2)
y <- rexp(n,1/mean(x))
s <- Surv(ifelse(x<y,x,y), x<=y)
plot(s, col=as.numeric(f))

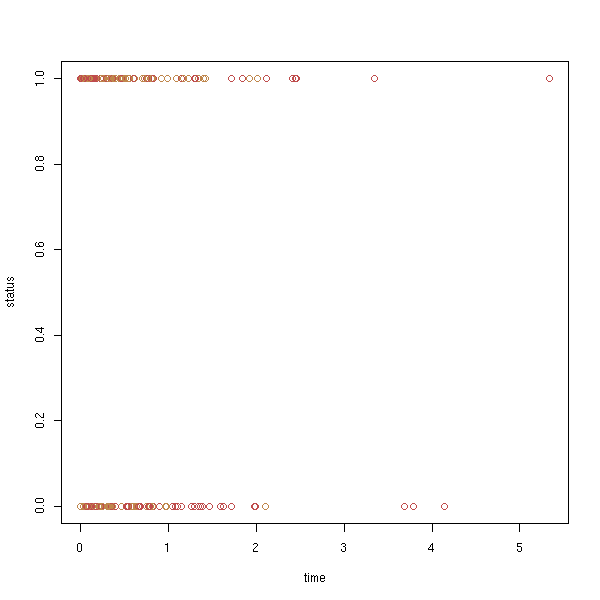
plot( density(s[,1][ s[,2] == 1 & f == 1]), lwd=3,
      main="Analyse de la survie, un facteur" )
lines( density(s[,1][ s[,2] == 0 & f == 1]), lty=2, lwd=3 )
lines( density(s[,1][ s[,2] == 1 & f == 2]), col='red', lwd=3 )
lines( density(s[,1][ s[,2] == 0 & f == 2]), lty=2, col='red', lwd=3 )
legend( par("usr")[2], par("usr")[4], yjust=1, xjust=1,
        c("non censored, f = 1", "censored, f = 1",
          "non censored, f = 2", "censored, f = 2"),
        lty=c(1,2,1,2),
        lwd=1,
        col=c(par('fg'), par('fg'), 'red', 'red') )

plot(survfit(s ~ f), col=as.numeric(levels(f)))

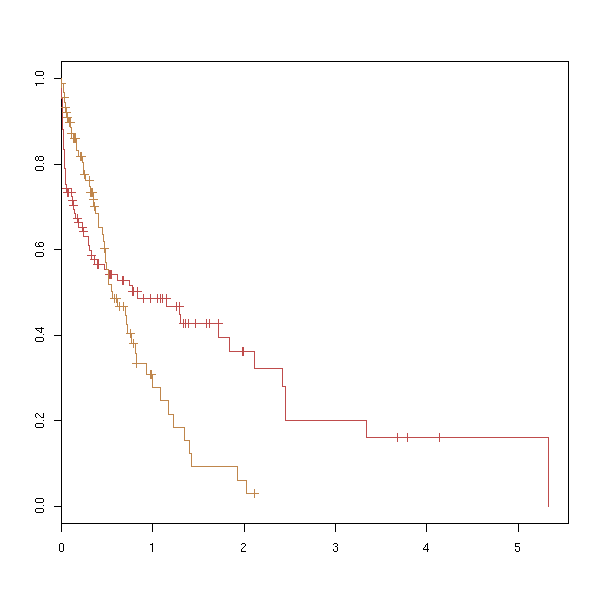
A FAIRE : avec deux facteurs
survfit(s~f1+f2)

A FAIRE : et si f n'est pas un facteur ??? (mettre ça un peu plus loin, quand on parlera de régression d'une variable de survie).

A FAIRE : choisir deux exemples, l'un avec l'autre sans covariables, que l'on utilisera jusqu'à la fin de ce chapitre.

data(lung)
x <- Surv(lung$time, lung$status)
plot(x)

plot(survfit(x))

LES LIVRES ET SUITE SUR LES FRACTALES

Splines cubiques et lissantes en R

Expression fonctionnelle entre le nombre d’or et la suite de Fibonacci:Modifier

Le calcul du $n$ -ième terme de la suite de Fibonacci via la formule de récurrence requiert le calcul des termes précédents. Au contraire, une expression fonctionnelle de la suite de Fibonacci est une expression où le calcul du $n$ -ième terme ne présuppose pas la connaissance des termes précédents. Binet a redécouvert une formule en 1843^{[réf. nécessaire]}, qui avait déjà été obtenue par de Moivre^{[réf. nécessaire]} en 1718 et par Euler en 1765^[4]. Cette expression fonctionnelle s'appelle la formule de Binet :

F_{n}={\frac {1}{\sqrt {5}}}(\varphi ^{n}-\varphi '^{n}),\qquad {\text{avec}}\qquad \varphi ={\frac {1+{\sqrt {5}}}{2}}\qquad {\text{et}}\qquad \varphi '={\frac {1-{\sqrt {5}}}{2}}=-{\frac {1}{\varphi }}.

Démonstration

Comme la suite de Fibonacci est linéairement récurrente d’ordre 2, son équation caractéristique est une équation du second degré :

x^{2}-x-1=0

dont les deux solutions sont :

\varphi ={\frac {1+{\sqrt {5}}}{2}}\qquad {\text{et}}\qquad \varphi '=-{\frac {1}{\varphi }}={\frac {1-{\sqrt {5}}}{2}}

où $φ$ est le nombre d'or. Les suites $(φ n)$ et $(φ' n)$ engendrent alors l'espace vectoriel des suites vérifiant $u n + 2 = u n + 1 + u n$ . Il en résulte que :

F_{n}=\alpha {}\varphi ^{n}+\beta \varphi '^{n}

F_{0}

F_1

Les conditions initiales $F_{0}=0$ et $F_{1}=1$ conduisent au système suivant :

\left\{{\begin{matrix}\alpha +\beta =0\\\alpha -\beta ={\frac {2}{\sqrt {5}}}\end{matrix}}\right.

On obtient alors :

\alpha ={\frac {1}{\sqrt {5}}}\qquad {\text{et}}\qquad \beta =-{\frac {1}{\sqrt {5}}}.

Nous obtenons finalement l'expression fonctionnelle recherchée.

(Ces calculs restent valables pour $n$ entier négatif quand la suite est prolongée comme ci-dessous.)

Quand $n$ tend vers $+\infty$ , $F_{n}$ est équivalent à ${\frac {\varphi ^{n}}{\sqrt {5}}}$ . Plus précisément, $φ n$ tend vers l'infini et $φ' n$ tend vers zéro car $|\varphi '|<1<\varphi$ .

La suite de Fibonacci comme limite d une fraction du nombre d’or

(Ces calculs restent valables pour $n$ entier négatif quand la suite est prolongée comme ci-dessous.)

Quand $n$ tend vers $+\infty$ , $F_{n}$ est équivalent à ${\frac {\varphi ^{n}}{\sqrt {5}}}$ . Plus précisément, $φ n$ tend vers l'infini et $φ' n$ tend vers zéro car $|\varphi '|<1<\varphi$ .

En fait, dès le rang $n = 1$ , le deuxième terme ${\varphi '^{n} \over {\sqrt {5}}}$ est assez petit pour que les nombres de Fibonacci puissent être obtenus uniquement à partir du premier terme :

F_{n}

Est l’entier le plus proche de

{\frac {\varphi ^{n}}{\sqrt {5}}}

Comme l'avait déjà remarqué Johannes Kepler^[6], le taux de croissance des nombres de Fibonacci, c'est-à-dire ${\frac {F_{n+1}}{F_{n}}}$ , converge vers le nombre d'or $φ$ .

En effet, puisque la suite $F_{n}$ est équivalente à ${\frac {\varphi ^{n}}{\sqrt {5}}}$ (cf. supra, section Expression fonctionnelle), la suite ${\frac {F_{n+1}}{F_{n}}}$ est équivalente à ${\frac {\frac {\varphi ^{n+1}}{\sqrt {5}}}{\frac {\varphi ^{n}}{\sqrt {5}}}}=\varphi ,$ qui est donc sa limite.

La suite de Fibonacci et les matrices :

Il existe d'autres démonstrations de la formule de Binet, telles que la transformation en Z et la technique des fonctions génératrices.

Remarquons qu'une fois découverte, cette formule se démontre aussi par récurrence (y compris pour $n$ entier négatif).

un autre manière de défit la suite de Finobacci matricielle ment est la suivante :

On a la relation de récurrence suivante : ${\begin{pmatrix}F_{n}\\F_{n+1}\end{pmatrix}}={\begin{pmatrix}0&1\\1&1\end{pmatrix}}{\begin{pmatrix}F_{n-1}\\F_{n}\end{pmatrix}}$ et donc ${\begin{pmatrix}F_{n}\\F_{n+1}\end{pmatrix}}={\begin{pmatrix}0&1\\1&1\end{pmatrix}}^{n}{\begin{pmatrix}F_{0}\\F_{1}\end{pmatrix}}$

Plusieurs formules existent notamment celle des nombres de Lucas ou par leur fonction génératrice :

Série génératriceModifier

La série génératrice de la suite de Fibonacci donne une série entière dont le rayon de convergence vaut 1/ $φ$ (d'après le théorème de Cauchy-Hadamard ou plus simplement, la règle de d'Alembert). Pour tout complexe z de module strictement inférieur à $1/ φ$ , la sériecorrespondante (absolument convergente) est égale à : $\sum _{n\in \mathbb {N} }F_{n}z^{n}={\frac {z}{1-z-z^{2}}}$

(donc à $z\sum _{m\in \mathbb {N} }(z+z^{2})^{m}=\sum _{m,k\in \mathbb {N} }{m \choose k}z^{1+m+k}$ , où les coefficients binomiaux $m \choose k$ sont nuls pour $k > m$ ).

Le triangle de Pascal et la suite de Fibonacci :

Propriété : $\forall n\in \mathbb {N} ,~F_{n}=\sum _{k\in \mathbb {Z} }{n-1-k \choose k}$ (somme finie car les coefficients binomiaux ${n-1-k \choose k}$ sont nuls si $k < 0$ ou si $k > n - 1 - k$ ).

Cette propriété se déduit immédiatement de l'expression de la série génératrice (voir supra). On peut aussi la démontrer par une récurrence d'ordre 2 sur $n$ .

ce qui signifie que dans Cela signifie que, dans un triangle de Pascal, les nombres de Fibonacci s'obtiennent en sommant les termes situés sur une diagonale (du bas vers la droite)

via RSS

#Dessins 1